ARTICLES

Snap to a Road

Wilfried Mestdagh's article shows how to take a lat/lon and find the nearest road relative to that point. The technique, written entirely in Delphi, employs reverse geocoding and determines the lat/lon using a CalcXY routine.

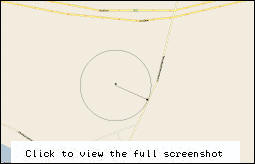
This article will show how to snap a position to a road. Many times a GPS receiver's calculated position is not as accurate as we should like it to be, and when you project the position in MapPoint by means of a pushpin the vehicle is not on the road.

Also a vehicle might be not on any (digitized) road at all, for example it can be on a field or a parking lot. In that case you don't want to snap it to a road but you maybe want information like: 'The vehicle is 20 meters south-east from streetname, streetnumber'. And this is exacly what the code given in this article will produce.

One warning is that if your application assumes a position that is not the real (actually the wrong) position that the GPS receiver gives you, you might get into trouble if customar is not fully informed of this assumption, so please be very clear on this. Getting wrong or mis-leading data is one thing, but letting an application make assumptions can get dangerous because it can be false information.

The best thing to do is make a vector with given increments, for example 5 meters, because most of the streets are wider. Then on the circumference of that circle we plot a point also every 5 meter until we hit a street or have completed the whole 360 degrees. Then we increment the radius with 5 meters and do it all over again.

This code example is written in Delphi, but even if you code in another language it should be fine readable for you. Afterall you're a programmer :).

First we create a little class named TMapPoint which handles the program's execution. This constructor creates a hidden MapPoint object because even if we have a visible map in the application we do not want to change it when this class is executing. There is only one public method:

function TMapPoint.GetStreetAddr(Lat, Lon: double; Streets: TStrings;
  out Direction: string; out Distance: integer): boolean;
var
   Angle: integer;
begin
   Streets.Clear;
   Distance := 0;
   Direction := '';
   if not FindAddr(Lat, Lon, Streets) then
      if CalcInCircle(Lat, Lon, Streets, Distance, Angle) then
         Direction := GetDirection(Angle);
   Result := Streets.Count > 0;
end; 

It first checks if the given coordinates are on a street calling FindAddr, if not then we see if we have a street in a given radius by means of CalcInCircle.

I'm not going to discuss the GetDirection function. All it does is divide the circle into 8 panes and return a string according to the angle, eg N, NE, etc.

The FindAddr encapsulates the MapPoint ObjectsFromPoint method:

function TMapPoint.FindAddr(Lat, Lon: double; Streets: TStrings): boolean;
var
   StreetResults: FindResults;
   Loc: Location;
   n, x, y: integer;
   Index: OLEVariant;
begin
   FMP.ActiveMap.GoToLatLong(Lat, Lon, 1);
   Loc := FMP.ActiveMap.GetLocation(Lat, Lon, 1);
   x   := FMP.ActiveMap.LocationToX(Loc);
   y   := FMP.ActiveMap.LocationToY(Loc);
   StreetResults := FMP.ActiveMap.ObjectsFromPoint(x, y);
   if StreetResults.ResultsQuality < geoNoGoodResult then
      for n := 1 to StreetResults.Count do try
         Index := n;
         Loc   := StreetResults.Item[Index] as Location;
         if Assigned(Loc.StreetAddress) then
            Streets.Add(Loc.StreetAddress.Value);
      except
      end;
   Result := Streets.Count > 0;
end;

The CalcInCircle function is the one that will try to find an address as close as possible within a given maximum radius:

function TMapPoint.CalcInCircle(CenterLat, CenterLon: double;
  Streets: TStrings; out Distance, Angle: integer): boolean;
var
   Lat, Lon: double;
   Radius: double;         // radius of the circle in degree
   Circum: integer;        // circumfence of the circle in Distance
   Count:  integer;        // the amount of points to calculate on the circumfence
   AngleInc: integer;      // angle increments in degree per calculation
begin
   Distance := FDistanceResolution;
   while Distance <= FMaxDistance do begin
      Radius   := 1 / 60 / 1852 * Distance;
      Circum   := Trunc(Distance * 2 * PI);
      Count    := Circum div FDistanceResolution;
      AngleInc := 360 div Count;
      if AngleInc <= 0 then begin
         Result := False;
         Exit;
      end;
      Angle := 0;
      while Angle < 360 do begin
         CalcXY(CenterLat, CenterLon, Angle, Radius, Lat, Lon);
         Result := FindAddr(Lat, Lon, Streets);
         if Result then
            Exit;
         Inc(Angle, AngleInc);
      end;
      Inc(Distance, FDistanceResolution);
   end;
   Result := False;
end;

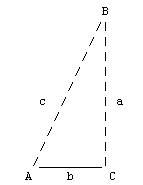
I think the rest is self-expanatory, so we only have to discuss the calcultion CalcXY itself:

   given A en c
   a = c * sin(A)
   b = c * cos(A)

• A == 0 is direction East in this drawing
• a is Latitude offset
• b is Longitude offset
• c is Radius of circle

procedure TMapPoint.CalcXY(centerLat, centerLon, Angle, Radius: double; out Lat, lon: double);
var
   a, b, c, r: double;
begin
   r := DegToRad(Angle);
   c := Radius;
   a := c * Sin(r);
   b := c * Cos(r) / Cos(DegToRad(centerLat));  // correct longitude for circle
   Lat := CenterLat + a;
   Lon := CenterLon + b;
end;

As you see it is used as in the above drawing to calculate a latitude / longitude pair of the points on the circumfence. We need the Cos function to correct longitude distance if we are not on the equator.

I might share an interesting word about the CalcInCircle function. As you see it gives up the search when it found 1 address. And yes in one of my applications it had to be that way, but in another one I had to give all addresses on the same circle if there was more than one. This can easy be done by adding a HitCount variable and instead of exit in the inner loop just increment that variable. This way it will allways finish the circle. And of course you exit the outer loop if HitCount is greater than zero.

I have dropped the complete code here in this textbox so you can easily copy it if needed. After all, so much of programming is just a copy / paste operation :).

	MP2Kmag Internet