 |
|
 |
 |
Determing Whether A Point Is Located Inside Polygon
Wilfried Mestdagh wrote this article on determing whether a vehicle is located inside or outside a convex polygon. "Simplify the polygon by make triangles from it one by one, until we have a triangle where the point is inside.
At the end we only have to verify if the point is in the last triangle."
Download code for this article.
| This article explains a method to calculate if a position is in or outside a convex polygon.
It does not make use of floating point numbers to optimize for speed as much as possible.
To transform Latitude / Longitude pairs into X/Y coordiantes, just multiply them with a given factor,
for example 100000. 1/100000 of a degree gives precision of around 1 meter which is already better than any GPS receiver.
|
| If you just want to download the complete project, included with demo executable
and source code then click here.
|
| To make the calculations easy we will reduce the polygon to triangles by replacing
each time two successive sides by a new one, provided that the triangle formed by the
two polygon sides and the new side does not contain the point.
|
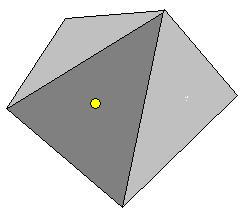
| Simplify the polygon by make triangles from it one by one, until we have a triangle where the point is inside.
|
| At the end we only have to verify if the point is in the last triangle.
|

| The last triangle.
|
| So we reduce the whole problem to a simple problem if a certain triangle a certain point
has in itself. Now, to move the triangle and also the point in such a way that the point is on the
origin of the coordinate axis (0,0) we again simplify the calculations.
|
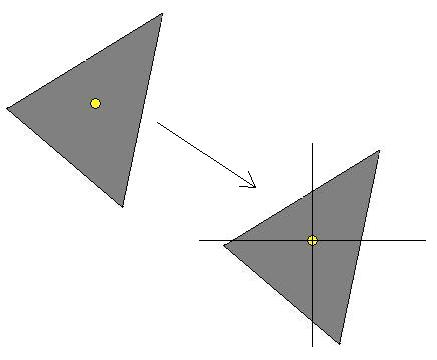
| Moving the polygon to the origin 0,0 of coordinates.
|
We search the sides intercepting the Y axis. If we don't find them then the zero point is certainly
not in the triangle. The 2 intercept points have to each be on another side of the X axis or on the X axis itself.
The calculation of a straight line going through the points X1, Y1 and X2, Y2 is:
z (x) = (y2 - y1) / (x2 - x1) x - (y2 - y1) / (x2 - x1) + y1
|
Now we have to see if the side is intercepting the Y axis. If x1 = x2 then this cannot be, so we can
drop the case. To find the intercept point of a straight line with the Y axis we find to compute z(0):
z(0) = (y1 - y2) / (x2 - x1) + y1
This intercept point is on the side and not on the straight line past the side if sng(x1 <> sng(x2).
|
Finally we have to find out if the side is intercepting the Y axis above or below the X axis. We
call the intercept point z(0) (see above). So we have to find the sign of x(0). So z(0) >= 0.
(y1 - y2) / (x2 - x1) * x1 + y1 >= 0
If x2 < x2, then x2 - x1 > 0 and then:
(y1 - y2) * x1 >= y1( - y2) [E1]
If x1 > x2, then x2 - x1 < 0, and then:
(y1 - y2) * x1 <= y1(x1 - x2) [E2]
So the intercept point is above the X axis if E1 or E2 is true.
|
| Below is the complete code written in Delphi. You can translate it into the programming language of your choice
and if you do so please post in the discussion thread for this article.
|
|
|










